
Numbers
A number is a mathematical object used to count and measure. A notational symbol that represents a number is called a numeral but in common use, the word number can mean the abstract object, the symbol, or the word for the number. In addition to their use in counting and measuring, numerals are often used for labels (telephone numbers), for ordering (serial numbers), and for codes (e.g., ISBNs). In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers.
Certain procedures that take one or more numbers as input and produce a number as output are called numericaloperations. Unary operations take a single input number and produce a single output number. For example, thesuccessor operation adds one to an integer, thus the successor of 4 is 5. Binary operations take two input numbers and produce a single output number. Examples of binary operations include addition, subtraction, multiplication,division, and exponentiation. The study of numerical operations is called arithmetic.
Different types of numbers are used in different cases. Numbers can be classified into sets, called number systems. (For different methods of expressing numbers with symbols, such as the Roman numerals, see numeral systems.)
| Natural | 0, 1, 2, 3, 4, ... or 1, 2, 3, 4, ... |
|---|---|
| Integers | ..., −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, ... |
| Positive integers | 1, 2, 3, 4, 5, ... |
| Rational | a⁄b where a and b are integers and b is not zero |
| Real | The limit of a convergent sequence of rational numbers |
| Complex | a + bi where a and b are real numbers and iis the square root of −1 |
Natural numbers
The most familiar numbers are the natural numbers or counting numbers: one, two, three, and so on. Traditionally, the sequence of natural numbers started with 1 (0 was not even considered a number for the Ancient Greeks.) However, in the 19th century, set theorists and other mathematicians started including 0 (cardinality of the empty set, i.e. 0 elements, where 0 is thus the smallest cardinal number) in the set of natural numbers.[citation needed] Today, different mathematicians use the term to describe both sets, including zero or not. The mathematical symbol for the set of all natural numbers is N, also written 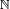 .
.
In the base ten numeral system, in almost universal use today for arithmetic operations, the symbols for natural numbers are written using ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. In this base ten system, the rightmost digit of a natural number has a place value of one, and every other digit has a place value ten times that of the place value of the digit to its right.
In set theory, which is capable of acting as an axiomatic foundation for modern mathematics,natural numbers can be represented by classes of equivalent sets. For instance, the number 3 can be represented as the class of all sets that have exactly three elements. Alternatively, in Peano Arithmetic, the number 3 is represented as sss0, where s is the "successor" function (i.e., 3 is the third successor of 0). Many different representations are possible; all that is needed to formally represent 3 is to inscribe a certain symbol or pattern of symbols three times.
Integers
The negative of a natural number is defined as a number that produces zero when it is added to the number. Negative numbers are less than zero, and are usually written with a negative sign (a minus sign). As an example, the negative of 7 is written −7, and 7 + (−7) = 0. When the set of the negatives of the natural numbers is combined with the natural numbers, the result is defined as the set of integer numbers, also called integers, Z also written 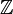 . Here the letter Z comes from German Zahl, meaning "number". The set of integers forms a ring with operations addition and multiplication.
. Here the letter Z comes from German Zahl, meaning "number". The set of integers forms a ring with operations addition and multiplication.
Rational numbers
A rational number is a number that can be expressed as a fraction with an integer numerator and a non-zero natural number denominator. Fractions are written as two numbers, the numerator and the denominator, with a dividing bar between them. In the fraction written m⁄n or
m represents equal parts, where n equal parts of that size make up one whole. Two different fractions may correspond to the same rational number; for example 1⁄2 and 2⁄4 are equal, that is:
If the absolute value of m is greater than n, then the absolute value of the fraction is greater than 1. Fractions can be greater than, less than, or equal to 1 and can also be positive, negative, or zero. The set of all rational numbers includes the integers, since every integer can be written as a fraction with denominator 1. For example −7 can be written −7⁄1. The symbol for the rational numbers is Q (for quotient), also written 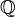 .
.
Real numbers
The real numbers include all of the measuring numbers. Real numbers are usually written using decimal numerals, in which a decimal point is placed to the right of the digit with place value one. Each digit to the right of the decimal point has a place value one-tenth of the place value of the digit to its left. Thus
represents 1 hundred, 2 tens, 3 ones, 4 tenths, 5 hundredths, and 6 thousandths. In saying the number, the decimal is read "point", thus: "one two three point four five six ". In the US and UK and a number of other countries, the decimal point is represented by a period, whereas in continental Europe and certain other countries the decimal point is represented by a comma. Zero is often written as 0.0 when it must be treated as a real number rather than an integer. In the US and UK a number between −1 and 1 is always written with a leading zero to emphasize the decimal. Negative real numbers are written with a preceding minus sign:
Every rational number is also a real number. It is not the case, however, that every real number is rational. If a real number cannot be written as a fraction of two integers, it is called irrational. A decimal that can be written as a fraction either ends (terminates) or forever repeats, because it is the answer to a problem in division. Thus the real number 0.5 can be written as 1⁄2 and the real number 0.333... (forever repeating threes, otherwise written 0.3) can be written as 1⁄3. On the other hand, the real number π (pi), the ratio of the circumference of any circle to its diameter, is
Since the decimal neither ends nor forever repeats, it cannot be written as a fraction, and is an example of an irrational number. Other irrational numbers include
(the square root of 2, that is, the positive number whose square is 2).
Thus 1.0 and 0.999... are two different decimal numerals representing the natural number 1. There are infinitely many other ways of representing the number 1, for example 2⁄2, 3⁄3, 1.00, 1.000, and so on.
Every real number is either rational or irrational. Every real number corresponds to a point on the number line. The real numbers also have an important but highly technical property called the least upper bound property. The symbol for the real numbers is R or 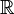 .
.
When a real number represents a measurement, there is always a margin of error. This is often indicated by roundingor truncating a decimal, so that digits that suggest a greater accuracy than the measurement itself are removed. The remaining digits are called significant digits. For example, measurements with a ruler can seldom be made without a margin of error of at least 0.01 meters. If the sides of a rectangle are measured as 1.23 meters and 4.56 meters, then multiplication gives an area for the rectangle of 5.6088 square meters. Since only the first two digits after the decimal place are significant, this is usually rounded to 5.61.
In abstract algebra, it can be shown that any complete ordered field is isomorphic to the real numbers. The real numbers are not, however, an algebraically closed field.








